√ 円 三角形 角度 167390

 こんにちは。 da Vinch (@mathsouko_vinch)です。 正弦定理と外接円正弦定理を紹介した時に外接円については触れなかったので、ここで少し確認したいと思います。まず「外接円」とは何かというと三角形の3つの頂点全てを通る Incoming Term 円 三角形 角度, 円 三角形 角度 高校, 円 三角形 角度 接線, 円 三角形 角度 中学, 円 三角形 角度 問題, 円 内接 三角形 角度, 円 外接 三角形 角度, 円 半径 三角形 角度,二等辺三角形の角についての問題は、こちらの記事でまとめているのでご参考ください。 ⇒ 二等辺三角形の角度の求め方を問題を使って徹底解説！ また、底角が等しいという性質は証明でも活用されます。 証明の中で二等辺三角形を見つけたら、

中学数学 円周角の定理 例題その４ 中学数学の無料オンライン学習サイトchu Su

円 三角形 角度

円 三角形 角度-答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺三角形に注目して を三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 （右図イのような場合も含めて）一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

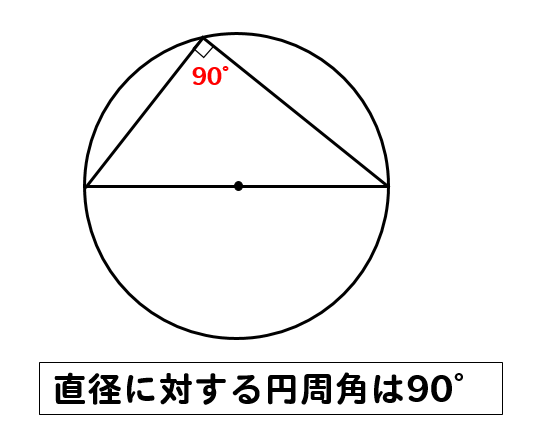
タレスの定理 （タレスのていり、 英 Thales' theorem ）とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理 、 タレースの定理 ともいう。入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。

入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 4年生 女子校 直角三角形 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺 同じように \(x\) 軸から測った角度 \(\theta\) の三角比はその点の座標になります。 三角比の値がマイナスになりますがこれは自然な三角比の拡張です。これが単位円を使った三角比の考え方でした。 では 180 度より大きくなっても大丈夫でしょうか。3年算数三角形教え方のポイント ① 三角形の仲間分け ② 二等辺三角形・正三角形の理解 ③ コンパス・定規を使っての二等辺三角形・正三角形のかき方 2年生の三角形の勉強 は 直角のところをみていました が、3年の三角形の勉強は、 辺の長さを特にみ

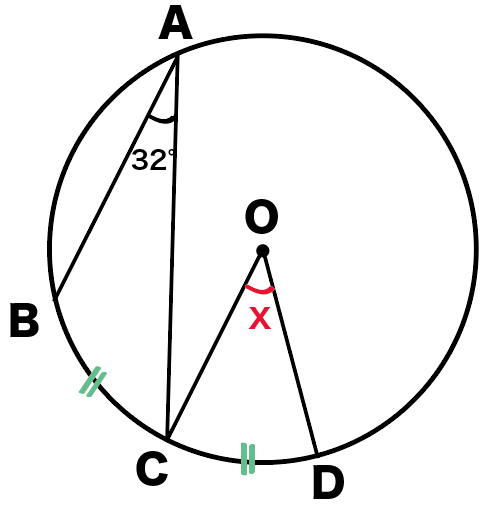
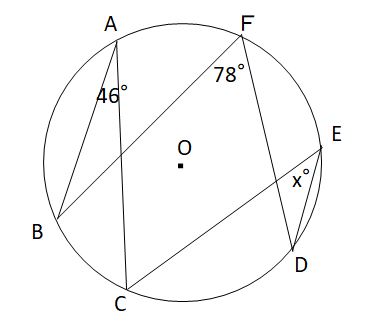
 円に内接する四角形の対角の和＝１８０°　（図４） ｘ＋ｙ＝ ｘ の中心角／２＋ ｙ の中心角／２＝３６０°/２＝１８０°外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円 でも中心角を頂角にする三角形が「二等辺三角形」ってことを利用すると・・・ つまり50°の半分、25°が円周角だね。 二等辺三角形の底角は等しいからxも25°。 円周角の求め方2

数学ａ 円周角と中心角の関係の使い方とコツ 教科書より詳しい高校数学

円周角の定理とは 必ず押さえたい７つのポイント 遊ぶ数学

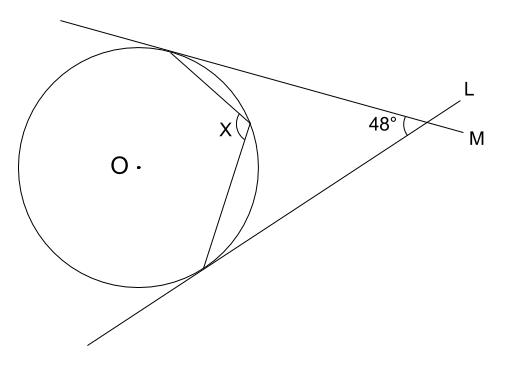
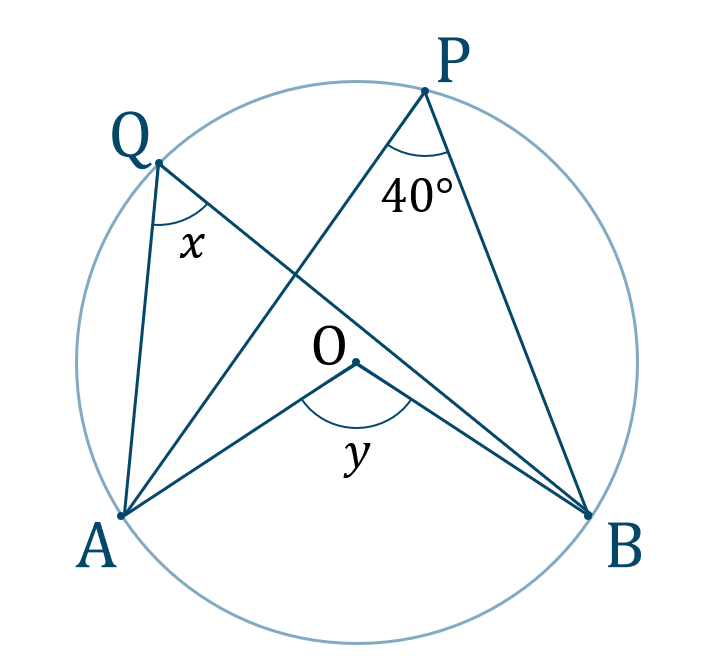
 七角形の謎。または一周はなぜ360度なのか Updated by Ryo Shimizu on , 1102 am JST 三角形の外接円の性質を使った問題の解法です。 外接円と聞いたら「二等辺三角形」という事を思い出せると良いですね。 円周角の定理を使って角度を求める問題です。 同じ弧を見つけることがポイントです。円の特徴 ここでは、同じ弦をもつ三角形に外接している円の特徴について説明しましょう。 図のように円の中に ABP、 AQB、 ABRがあるとします。 この三角形はABを共通の底辺としてもっていますね。 このような状況にあるとき、∠APB＝∠AQ

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

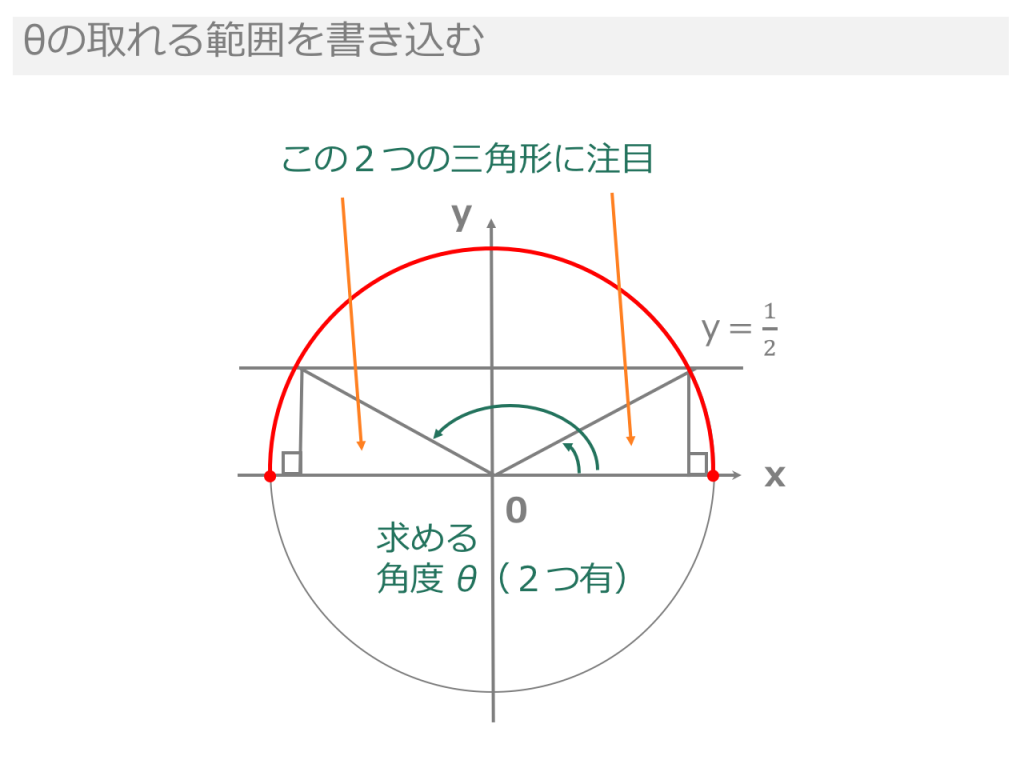
 三角形の内接円、外接円、面積、角度 外接円の中心と半径を求めるコードを作ってみました。 公式がわからなかったので、 Wikipedia の外接円の項目を参照しました。 (x1)^2 (y2)^2=3^2という円の方程式の形で結果を出力します。 小数の場合は小数点以下2桁入力と同時に計算可能な角度、長さを算出します。 ・立体図形では底面積と高さから体積を求めます。また、体積と底面積から高さを求めることもできます。 対応図形 ・直角三角形 ・三角形 ・扇型 ・円 ・楕円 ・三角すい ・三角柱 ・円すい ・円柱 このように、三角関数の角度は単位円に条件を書き込んでいくだけで求められます。 範囲や値の条件を見落とさないようにすることだけ注意しましょう！ 三角関数の角度の計算問題 それでは、実際に三角関数の角度の計算問題を解いていきましょう！

内接円 内心

円周角の定理の解説 問題の解き方 数学fun

②接点三角形←→接線三角形 （内接円の） ③垂足三角形←→傍心三角形 （角度）・・・これが意外でした。 ④チェバ三角形←→逆チェバ三角形 （楕円の） s：これらはみな同じ「三角形からできる三角形」の構造ということですね。 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ＝となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質 円 内接 三角形 角度 円 内接 三角形 角度 2月 13, 21 外接円、内接円などは三角比とともに融合されてよく出てきますが、1つひとつ確認していきましょう。 例題1では角度につい

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

円周角と比の問題 苦手な数学を簡単に

内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ～ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離 下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2＝360°になります。 ですのでaの角度は、360°(72°38°30°)＝2° よって、 答え a＝2 °他の説によれば 1 度は正三角形の角度の 60 分の 1 であることである。 バビロニアの天文学者やそれに続くギリシャの天文学者が使用した初期の三角法は 円の弦に基づいている。 半径に等しい弦は自然な基準量 (base quantitiy) となる。

1

円周角の定理はこれで完璧 定理の証明と様々な問題の解法

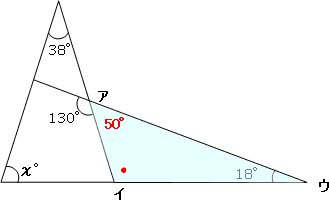
□×2＝180－115＝65度 ○×2＋●×2＋□×2＝ (三角形の内角の和)＝180度 よって ○×2＋●×2＝180－□×2＝180－65＝115度 イ＝○＋● なので イ＝ (○×2＋●×2)÷2＝115÷2＝575度三角形の重心の性質 b 24 三角形の三中線は重心で交わり、重心は各中線 を2 1 に内分する ag∶gd=bg∶ge=cg∶gf=2∶1 21 円に内接する四角形の対角の和 a ab ch = 2 1 25 = 180° 22 円の共接線の長さ c ab=2√r×r 23 接弦定理a ① 鋭角のとき（∠BAT ＜ 90°） 初めに、円の接線 A T と弦 A B が作る角 ∠ B A T < 90 ° のとき。 まず、 A D が円の直径になるように、点 D をとります。 ここで、三角形 A B D に注目すると、以下の4つの式が成り立つことが分かります。

円と三角形 角度 中学から数学だいすき

円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

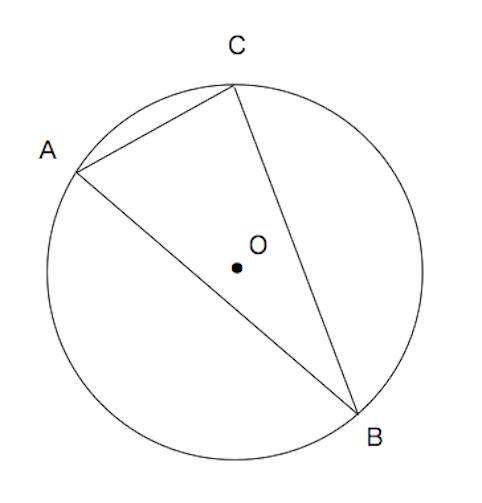
三角形の3辺から角度を計算 答えの度分秒（° ′ ″ ）は、秒の小数点以下2桁まで求めています。 台形型の部屋の変形のコーナーに壁にピッタリと合った棚を作ろうと思い図面を牽きましたが角度の算出方法が分からずお世話になりました、凄く助かり円周角は中心角の半分（中心角は円周角の２倍）だから x=2× (31°17°)=96° （答）問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

円周角の定理の基本 計算 無料で使える中学学習プリント

 三角形を描く 三角形の角度は60度＋60度＋60度 再度立ち上げます。 python 「turtle」をインポートします。 >>> import turtle 書いていきましょう。 >> > turtleleft(1) 左に1度の角度でカーソルが現れました。 ちなみに右に1度にするとこうなる。>>> turtleright(1

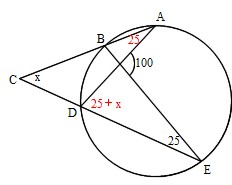
Mathematics 円 ４ 円周角の難しい問題を解くコツ 働きアリ

角度 直径と円周角 中学から数学だいすき

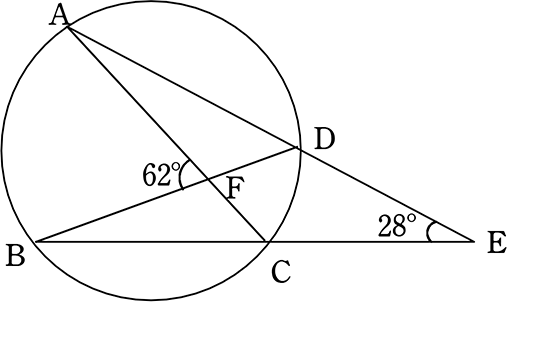
中学数学 円周角 中心角

面積の移動 円周角 知能問題 数的処理 判断推理 数的推理 数学パズル ｓｐｉ 空間把握 解いてみてください

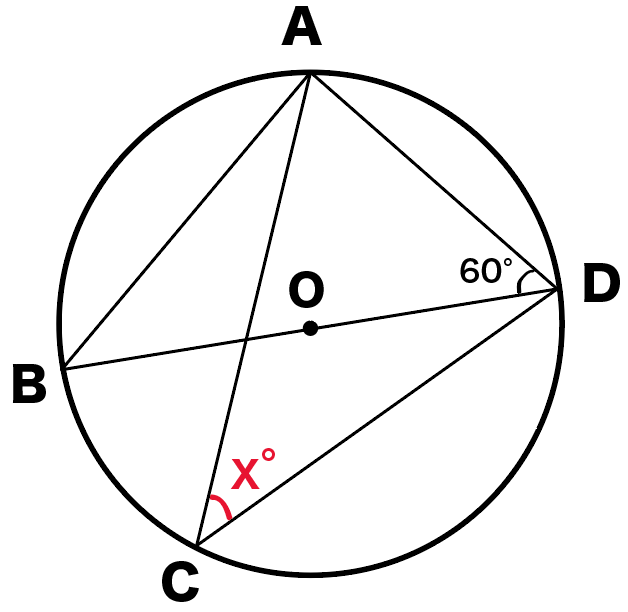
円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

円の中からはみ出ている三角形の問題はどう解けばいいですか 角度x角度yを Yahoo 知恵袋

これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ

角度の求め方 算数の教え上手 学びの場 Com

中3数学 円周角の角度を求めるポイントと練習問題 中学生勉強サイトあかね先生

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

勉強しよう数学0 11

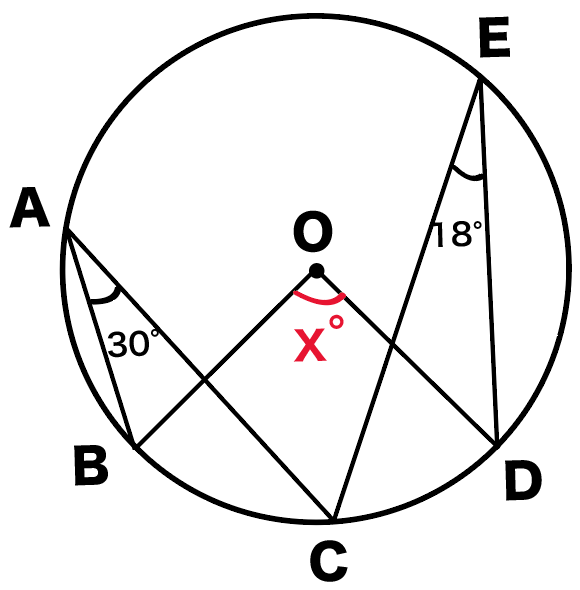
円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学

円周角

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

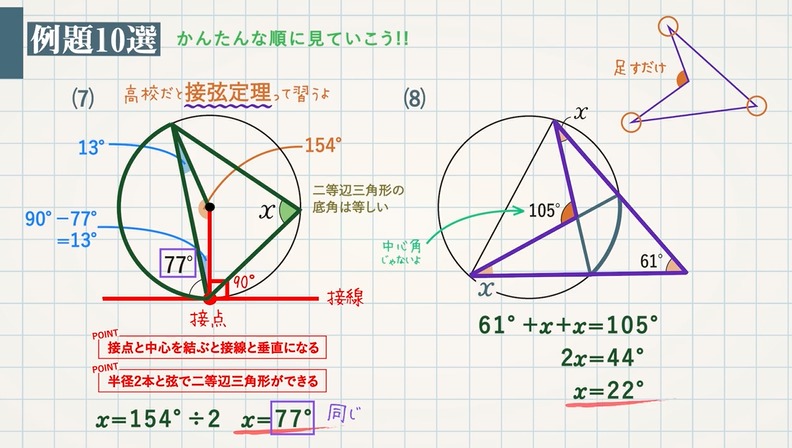
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

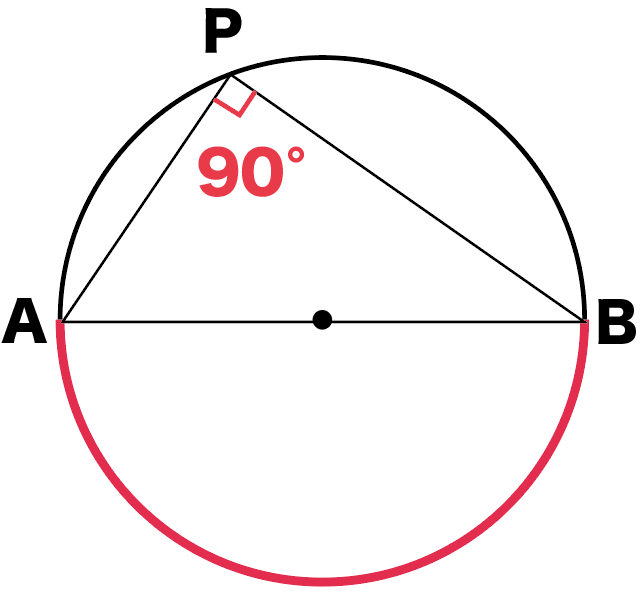
中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく

円の中にある三角形の角度の求め方です 上の円の角oac Adcと下の円の角 Yahoo 知恵袋

数学 中3 59 円周角の証明チャレンジ Lv 1 Youtube

円周角

中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット

数学 中3 56 円周角の定理 基本編 Youtube

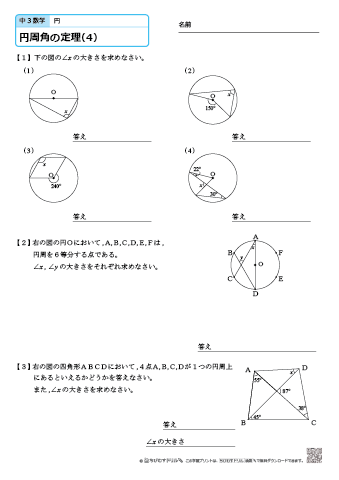
中学３年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生

3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

接弦定理の証明 円周角が鋭角ver 数学a By となりがトトロ マナペディア

円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

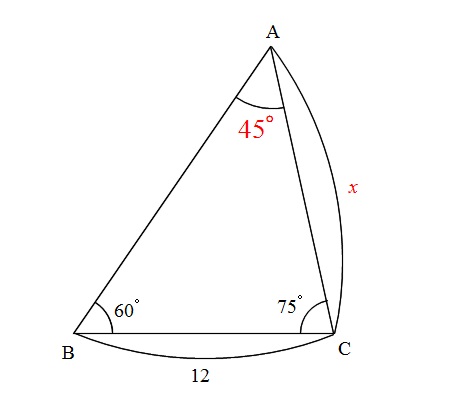
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

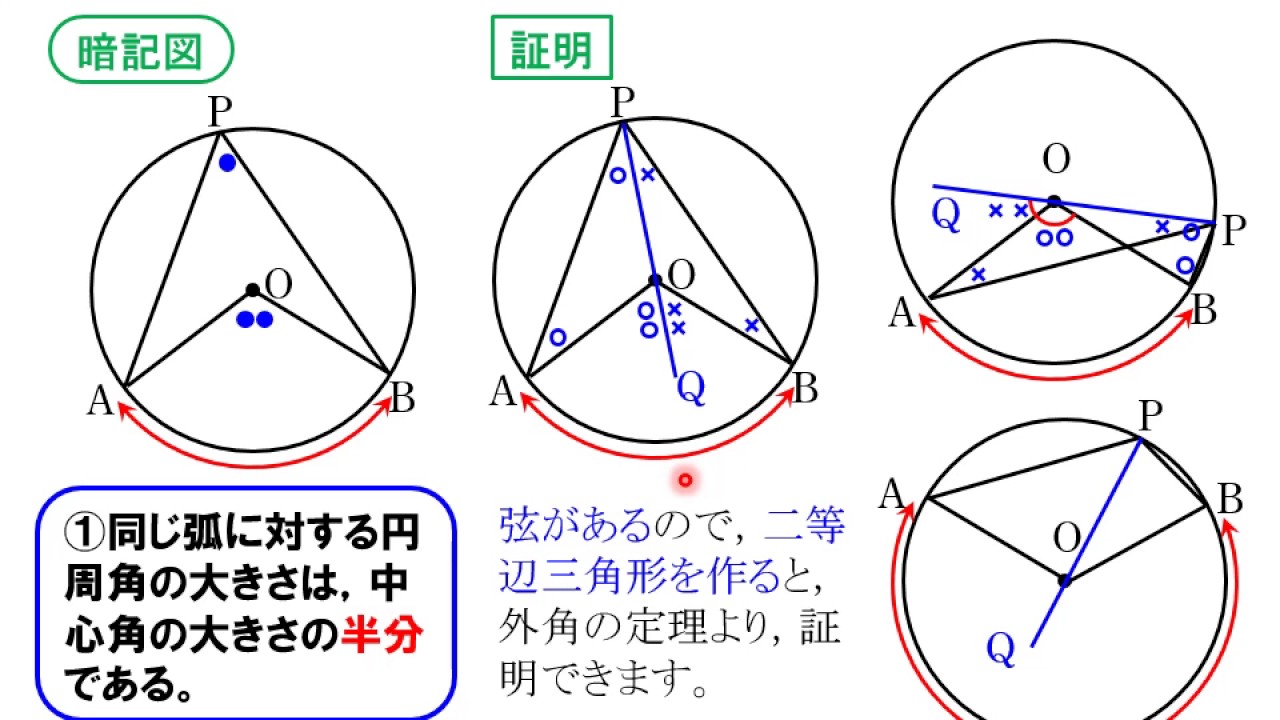
同じ弧に対する円周角

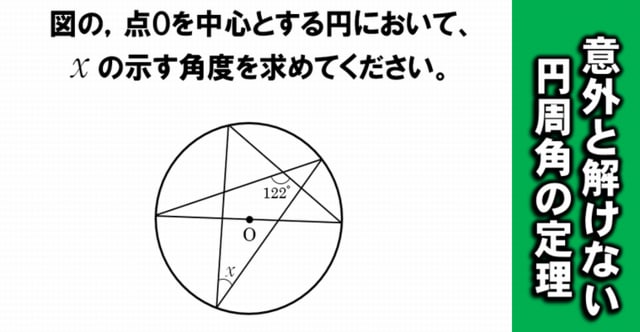
意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ

円と三角形 角度２ 中学から数学だいすき

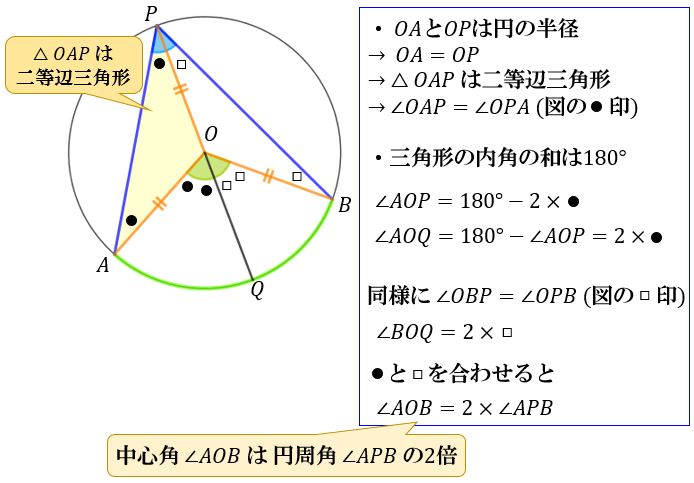
円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ

角度の求め方 算数の教え上手 学びの場 Com

中３で学習する 円 の単元で円周からはみ出している角度を求めるにはどうし Yahoo 知恵袋

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

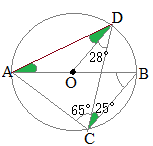
円周角の定理 入試問題

Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear

中学数学 円周角の定理 例題その４ 中学数学の無料オンライン学習サイトchu Su

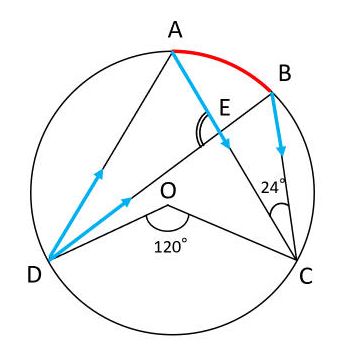
円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest

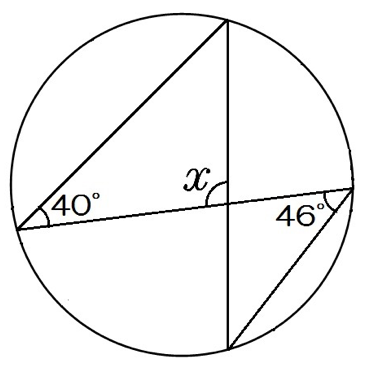
円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

円と三角形 角度 中学から数学だいすき

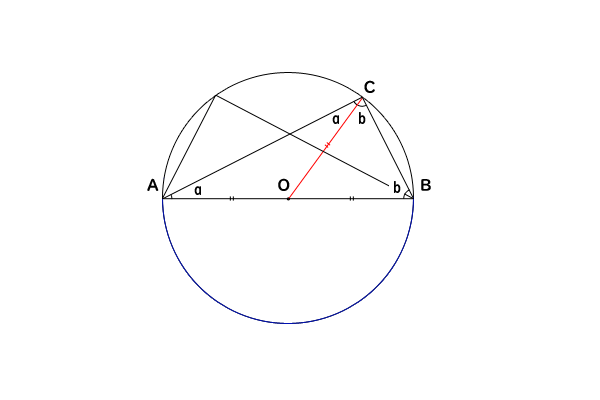
円周角の定理とその逆の証明 高校数学マスター

円の特徴 同じ弦をもつ三角形 数学a By Okボーイ マナペディア

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

円周角と円の外の点を結んで おときち副塾長 電脳空間学習塾かもん Youtube

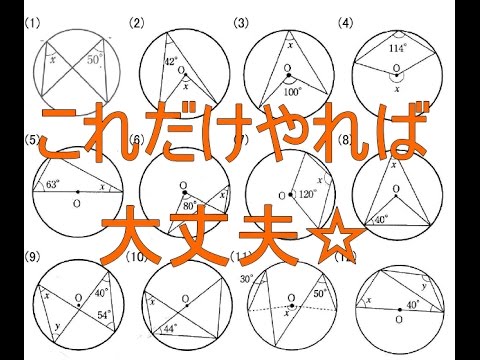
円周角の定理と中心角 中学３年数学 Youtube

1

三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

中学数学 円の中の三角形の角度の問題 お世話になります 円の中の三角形 Okwave

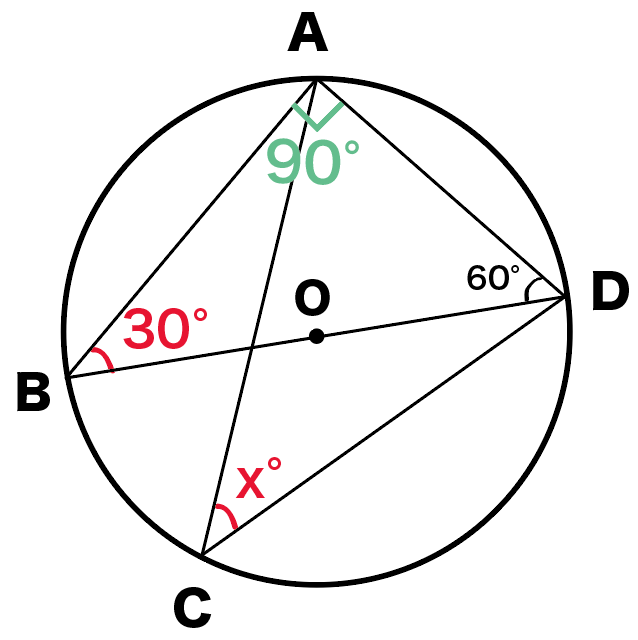
円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4

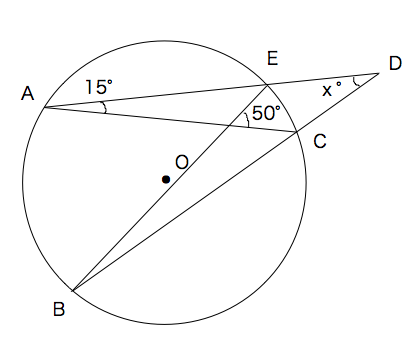
円周角の定理 練習問題 苦手な数学を簡単に

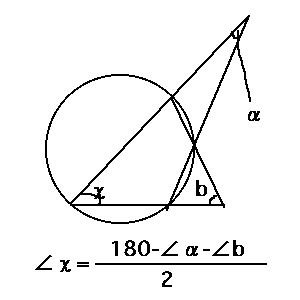
角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

円周角の定理 円に内接する四角形等図形の練習問題 中学 高校数学 身勝手な主張

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題

円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典

円と角度02 円周角の性質 Youtube

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

1

1

三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

中3数学 円の角度の求め方 例題編 映像授業のtry It トライイット

円周角

中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

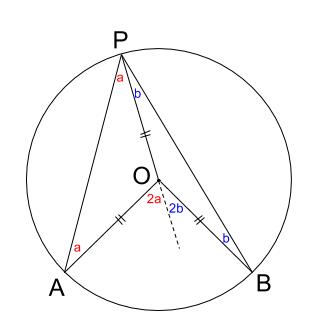
中学数学 円周角の定理はなぜ成り立つのか 中学数学の無料オンライン学習サイトchu Su

円と三角形 角度２ 中学から数学だいすき

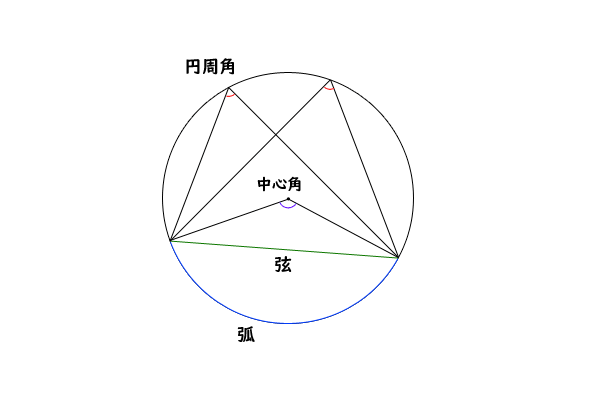
円周角の定理とその逆の証明 高校数学マスター

円の接線と角度 中学から数学だいすき

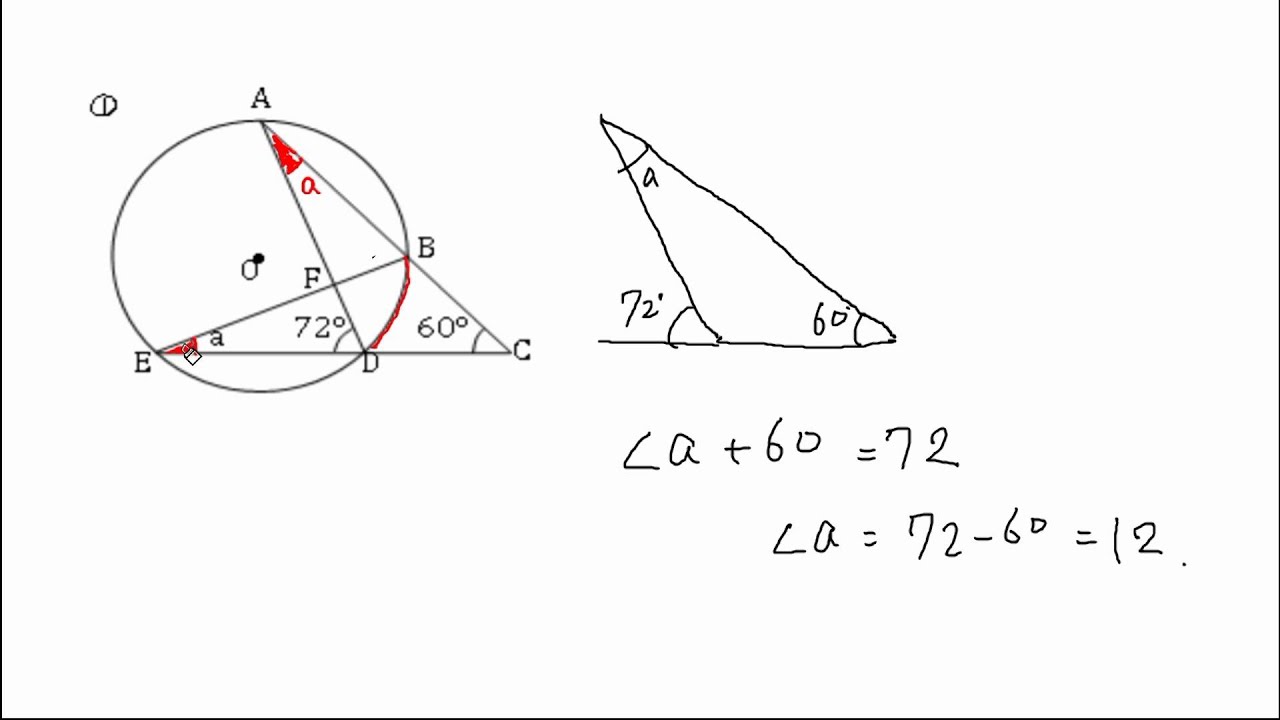
円周角の定理 問題 Youtube

角度 円と三角形 中学から数学だいすき

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

数学 中3 57 円周角の定理 少し応用編 Youtube

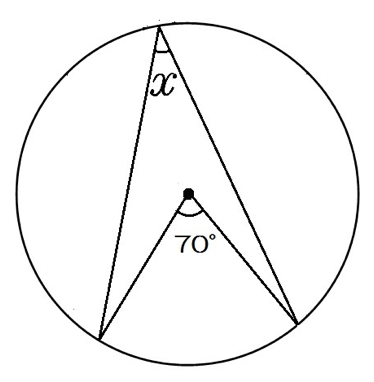
円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

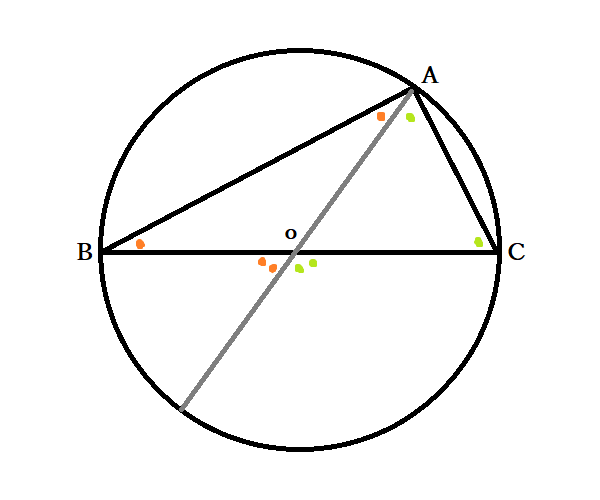
中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog

Mathematics 円 ４ 円周角の難しい問題を解くコツ 働きアリ